(书接上文)本章要点:
3. 一个关键方法 (如何列写KVL方程)
如果这一题你可以轻松地解答,本文可以忽略。

电路方程的结构由几何约束确定,即KCL或KVL,而又以KCL方程最常用,且容易出错,所以列写KVL方程是电路分析最关键的基本功。KVL方程的形式为: ±∑ U ±∑ IR =0 ,关键是正负号如何确定。关键在于如何理解电压循行方向。提到KVL自然会想到电压循行一周,而且还有“遇正则正,一致则正”的KVL口诀,然而通常并不能解决根本问题,列写时还是容易出错。摔锅认为要从两点理解:
(1)KVL 的本质是比较关系的传递;
(2)电压循行是电压参考方向箭标表示法的形式之一。
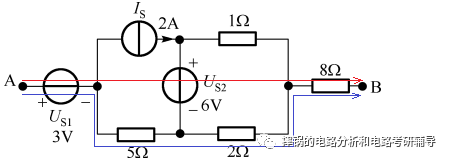
UAB可以用剪标表示,如图所示,红色和蓝色的剪标都可以。红色从A直接指向B,即两点电位的直接比较,这是我们通常理解的电压参考方向的剪标表示法。蓝色从A途经一系列元件最后指向B,这就是电压的循行,本质是比较关系的传递。举例解释:假如有ABCD四人, 如果你知道A比B高多少,B比C高多少,C又比D高多少,你自然可以根据这三个关系得到A比D高多少。所以KVL定律很容易证明,其实就是说:已知A比B高多少,B比C高多少,C比D高多少,D比A高多少,这样传递比较,那么A比A高多少?那还用问吗?显然等于0喽,所以有KVL方程 ∑ U=0
基于上述两点理解,电压循行的思路就清晰了。当然列写时,还要灵活运用两种约束先求出每一个元件的电量。蓝色循行路径中,关键要求出5欧和2欧电阻的电流或电压,此不再赘述。最后列写方程时应用口诀“遇正则正,一致则正”,前者针对±∑ U项,后者针对±∑ IR项。








